تصور کنید سه ردیف عدد زیر هم به ما داده شده است که ادعا میشود ردیف سوم حاصل جمع دو ردیف اول است.
این عملیات در پسزمینه انجام میگیرد که کنترل آن خارج
از اختیار ما است و خروجی آن لزوما نشانگر جمع صحیح نیست. اما میتوانیم هر تعداد
ستون دلخواه از آن را حذف کنیم تا به جمع درستی برسیم. به عنوان نمونه، در مثال زیر
میتوانیم با حذف ستونهای دوم و چهارم به جمع درستی برسیم:
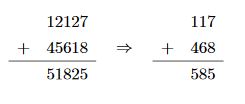
ماموریت شما یافتن حداقل تعداد ستونهایی است که با حذف
آنها عبارت محاسباتی درست است.
ورودی برنامه
[برگرد بالا]
هر دسته ورودی برنامه با یک عدد مثبت $n$ نابیشتر از
$1000$ آغاز میشود که بیانگر تعداد ستونهای اعداد است و پس از آن سه سطر شامل سه
عدد با آن تعداد رقم میآید. این اعداد به ترتیب دو عدد ورودی عملیات جمع چندستونی
و عدد خروجی آن هستند. ورودی زمانی پایان میابد که عدد صفر برای تعداد ستونها
ارسال شود.
3
123
456
579
5
12127
45618
51825
2
24
32
32
5
12299
12299
25598
0
خروجی برنامه
[برگرد بالا]
به ازای هر دسته ورودی تنها یک عدد در سطر مجزا چاپ شود
که حداقل ستونهای مورد نیاز برای حذف را نشان میدهد.
0
2
2
1
منبع: مسابقه برنامهنویسی ACM-ICPC
منطقهای سایت تهران 2017 -
مسئله Column Addition
حل مسئله
[برگرد بالا]
هر انتخابی از ستونها ممکن است ما را به جواب برساند. در
واقع هدف ما انتخاب کوچکترین زیرمجموعه از مجموعه ستونها است که با حدف آنها، حاصل
جمع به درستی محاسبه شده باشد. سادهترین راهکار ممکن برای حل مسئله آن است که تمام
حالات ممکن برای حذف ستونها را بررسی کنیم. هر مجموعه با $n$ عضو $2^n$ زیرمجموعه
دارد. بنابراین اگر بخواهیم در این مسئله تمام زیر مجموعههای ممکن را بررسی کنیم،
در بدترین حالت باید $2^{1000}$ زیرمجموعه پردازش کنیم که در عمل غیر ممکن است.
در این انتخابها باید این موضوع را نیز در نظر داشته
باشیم که بود یا نبود یک ستون مستقل از سایر ستونها نیست و رقم نقلی ستون قبل نیز
در آن نقش داشته و وجود یا عدم وجود آن در رقم نقلی انتقالی به ستون بعدی اثر دارد.
نکته دیگر آن است که وجود یا عدم وجود برخی ستونها قطعی است. به عنوان نمونه، اگر
دو عدد 2 و 5 جمع زده شده و خروجی 9 تولید شده باشد، این ستون حتما باید حذف شود؛
یا ستونهایی از سمت راست که با رقم نقلی صفر به درستی جمع زده شدهاند، قطعا نباید
حذف شوند (چرا؟). اما چنین پیشپردازشهایی لزوما جواب نهایی را تولید نکرده و ما
همچنان نیاز به الگوریتم بهینه برای حل مسئله داریم. بهتر است این الگوریتم به
گونهای طراحی شود که حالت استثناء نداشته و متکی به پیشپردازش نباشیم. مثال زیر
نمونهای است که پیشپردازشهای فوق روی آن اثری ندارند و کمکی به ما نمیکنند.
111119
111119
322228
ایده دیگر برای حل مسئله آن است که یک الگوریتم حریصانه طراحی کنیم. در الگوریتم حریصانه هر انتخاب
بدون توجه به انتخابهای قبلی و بعدی است و تنها شرایط حال حاضر در نظر گرفته
میشود. با توجه به آنکه با عملیات جمع سر و کار داریم و شرایط حال حاضر هر ستون به
ستون قبل از خود وابسته است، پس انتخاب ستونها را از سمت راست شروع کرده و اگر
ستونی جمع ستونهای قبلی را به هم بزند، آن را حدف میکنیم. منظور از به هم زدن آن
است که با توجه به رقم نقلی و مقادیر ستون، جمع به درستی انجام نشود. این حالت در
هر سه نمونه ورودی درست جواب میدهد. به عنوان مثال، با شروع از کمارزشترین رقم
دومین ورودی نمونه، ابتدا ستون دوم و سپس ستون چهارم بر اساس این قانون حذف
میشوند. اما این راهکار در مورد مثل فوق جواب درست نمیدهد. چرا که ستون اول را به
عنوان یک محاسبه درست انتخاب کرده و بقیه ستونها را تا ستون آخر به خاطر ناسازگاری
با آن حذف میکند. در نتیجه با این روش چهار ستون حذف میشوند. در حالی که با حذف
کردن تنها دو ستون اول و آخر نیز به جواب درستی میرسیدیم.
در مرحله بعد به سراغ الگوریتمهای برنامهنویسی پویا میرویم. همانگونه که در بند اول نیز توضیح
داده شد، این مسئله در واقع انتخاب یک زیرمجموعه کمینه از مجموعه ستونها است که
شرط مسئله را بر اساس محدودیتهای عمل جمع برآورده کنند. مسئله کولهپشتی صفر و یک
نیز نمونه دیگری از مسائل انتخاب زیرمجموعه بهینه است. بنابراین شاید بتوان با
الگوریتمی مشابه آنچه که مسئله کولهپشتی صفر و یک به روش برنامهنویسی پویا حل شده
است به نتیجه رسید.
در حل مسئله کولهپشتی صفر و یک با $n$ کالا و حداکثر بار
قابل تحمل $W$، ماتریس $M$ با ابعاد $(n+1) \times (W+1)$ داریم که عدد عنصر
$M_{ij}$ حداکثر ارزش قابل حمل در کولهپشتی از بین $i$ کالای اول با محدودیت مجموع
وزن $j$ است. ماتریس خط به خط و خانه به خانه پر میشود تا به عنصر $M_{nW}$ برسیم
که بهترین جواب ممکن را نشان میدهد. نقش داشتن یا نداشتن یک کالا در انتخاب بهینه
نیز وابسته به انتخاب کالاهای قبلی و میزان وزن باقیمانده قابل تحمل کولهپشتی است.
در مسئله حال حاضر نیز $n$ ستون داریم که باید تعدادی را برای باقی ماندن انتخاب
کنیم و در نهایت حذفها به نحوی باشد که علاوه بر درست بودن عملیات جمع ستونها،
رقم نقلی آخرین ستون نیز صفر باشد.
با توجه به آنکه رقم نقلی ستونها در این
عملیات تنها یکی از دو عدد صفر یا یک است (چرا؟)، ماتریس $M$ برای این مسئله
میتواند یک آرایه دو بعدی با ابعاد $ 2 \times (n + 1)$ باشد. عددی که در خانه
M[i][j] نوشته میشود، بیانگر حداقل تعداد ستونهای حذف شده از $j$ ستون اول اعداد
(شمارش از سمت راست) با شرط تولید رقم نقلی $i$ است. ستون اول ماتریس $(j=0)$
بیانگر حالتی است که هیچ ستونی وارد عملیات پردازش نشده است. بدیهی است در این حالت
رقم نقلی صفر است و چون ستونی نداریم، مقدار M[0][0] (کمترین ستون حذف شده تا این
لحظه) صفر میشود. از سوی دیگر، امکان ندارد در چنین شرایطی رقم نقلی یک تولید شود.
در این حالت انتخاب یا عدم انتخاب ستون مطرح نیست و در واقع با شرایطی مواجه هستیم
که در کل باید کنار گذاشته شود. پس M[1][0] را $n$ قرار میدهیم. این عدد یا هر عدد
بزرگتر از آن جریمهای است که باعث میشود این حالت در طی محاسبات برای یافتن جواب
بهینه به صورت خودکار حذف شود. چرا که حداکثر تعداد ستونهای قابل حذف (بدترین جواب
ممکن) همان $n$ است.
پس از مقداردهی ثابت ستون اول، سایر ستون ها یک به یک بر
اساس قوانین زیر از روی مقادیر ستون قبلی پر میشوند. در ادامه منظور از $a$، $b$ و
$c$ به ترتیب ارقام اول تا سوم یک ستون از عملیات جمع هستند.
1- مقدار M[0][j]: اگر ستون $j$ برای ماندن انتخاب نشود،
تعداد M[0][j-1] ستون قبل از آن حذف شده که در نهایت رقم نقلی صفر تولید شده و با
حذف این ستون باید یک واحد به آن اضافه شود. اگر این ستون انتخاب شود، سه حالت ممکن
است اتفاق بیفتد. اگر $a + b$ برابر $c$ باشد، از ستونهای قبلی باید حالتی را در
نظر بگیریم که رقم نقلی صفر به این ستون رسیده باشد که با M[0][j-1] ارتباط دارد.
اما اگر $a + b$ یک واحد کمتر از $c$ باشد، برای انتخاب باید رقم نقلی یک از
ستونهای قبلی به این ستون رسیده باشد که با M[1][j-1] مرتبط است. در غیر از این دو
حالت، غیر ممکن است که جمع به درستی انجام شده و رقم نقلی صفر نیز به ستون بعدی
منتقل شود. در این شرایط باید مقدار $n$ لحاظ شود. حال که وضعیت ستون در دو حالت
انتخاب یا عدم انتخاب را بررسی کردیم، کمترین مقدار بین این دو عدد، مقداری است که
در M[0][j] قرار داده میشود:
\[ M[0][j]= min(M[0][j-1] + 1, t) \]
\[t = \left\{\begin{matrix} M[0][j - 1] & &
& if \; a + b = c\\ M[1][j - 1] & & & if \; a + b + 1 = c \\ n
& & & Otherwise \end{matrix}\right. \]
2- مقدار M[1][j]: به همان ترتیب فوق، اگر ستون $j$ برای
ماندن انتخاب نشود، تعداد M[1][j-1] ستون قبل از آن حذف شده که در نهایت رقم نقلی
یک تولید شده و با حذف این ستون باید یک واحد به آن اضافه شود. اگر این ستون انتخاب
شود، سه حالت ممکن است اتفاق بیفتد. اگر $a + b$ دو رقمی بوده و رقم یکان آن برابر
$c$ باشد، از ستونهای قبلی باید حالتی را در نظر بگیریم که رقم نقلی یک به این
ستون رسیده باشد که با M[0][j-1] ارتباط دارد. اما اگر $a + b + 1$ دو رقمی بوده و
رقم یکان آن برابر $c$ باشد، برای انتخاب باید رقم نقلی یک از ستونهای قبلی به این
ستون رسیده باشد که با M[1][j-1] مرتبط است. در غیر از این دو حالت، غیر ممکن است
که جمع به درستی انجام شده و رقم نقلی یک نیز به ستون بعدی منتقل شود. در این شرایط
باید مقدار $n$ لحاظ شود.
\[ M[1][j]= min(M[1][j-1] + 1, t)\]
\[t = \left\{\begin{matrix} M[0][j - 1] & &
& if \; a + b > 9 \; and \; (a+b) \; \% \; 10 = c\\ M[1][j - 1] &
& & if \; a + b + 1 > 9 \; and \; (a + b + 1) \; \% \; 10 \;= c \\ n
& & & Otherwise \end{matrix}\right. \]
پس از اتمام عملیات پر کردن آرایه، مقدار M[0][n] پاسخ
بهینه مورد نظر ما است (چرا؟). در ادامه ماتریس پر شده برای نمونه دوم ورودی برنامه
و همینطور مثال نقض الگوریتم حریصانه آمده است.
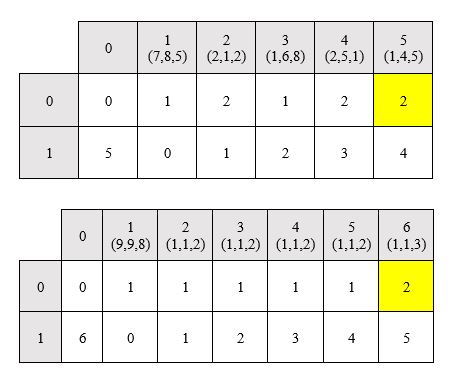
بر اساس توضیحات و اینکه صرفا ماتریس با تعداد سطرهای
ثابت را پر میکنیم، الگوریتم پیشنهادی از مرتبه پیچیدگی $O(n)$ است که نشان از
کارایی مطلوب آن دارد.